senesceR: Simulating cell populations undergoing the transition from proliferation competence to replicative senescence

Installing package

The R package is available at its R-forge page:

http://r-forge.r-project.org/projects/senescer

Since large parts of this package are a set of R functions wrapping a set of C++ functions, there are issues with compiling this package from scratch, particularly under Windows. Currently I recommend using senesceR under Linux only. To install and build from source:

• Check out the package source code from the R-forge SVN repository.
• Ensure that GSL is installed on your system. For example, using apt-get, run the following command in the shell: sudo apt-get install libgsl0-dev
• senesceR depends on two other R packages: Rcpp and RcppGSL. To make these available, in an R session run: install.packages(c("Rcpp","RcppGSL")).
• Finally, return to the shell, navigate into the senesceR directory checked out by SVN and simply run make install

Introduction

Cell passage experiments to observe cells undergoing the transition from proliferation competence to replicative senescence are difficult and time-consuming. Population growth masks single cell level dynamics, which are probably the most informative for learning about biological processes. SenesceR is a computer simulation of populations of cells in a container dividing stochastically until they become confluent. In passage experiments, once confluence is reached a subsample of cells is taken and transferred to an empty flask to continue dividing. SenesceR repeatedly simulates passaging until no more cells can divide and the population is completely senescent.

Model summary

Individual daughter cells inherit division potentials (number of divisions achievable before replicative exhaustion) from their mothers, suitably reduced to simulate telomere shortening. Starting division potentials can be generated according to the commitment theory of cellular senescence (Kirkwood and Holliday), sampled from a distribution or be fixed for all cells. Model output includes population distribution of cell division potentials at all times (and population doubling numbers) from the start of the simulated experiment until all cells have become senescent. This includes the number (and so fraction) of senescent cells, for which division potential = 0. Simulation of one population to complete replicative exhaustion provides a single measure of population division potential: population doublings until senescence, commonly referred to as the Hayflick limit and commonly measured in cell culture assays. Repeated stochastic simulations can provide information about Hayflick limit distribution in response to underlying model assumptions and parameter values.

Model output

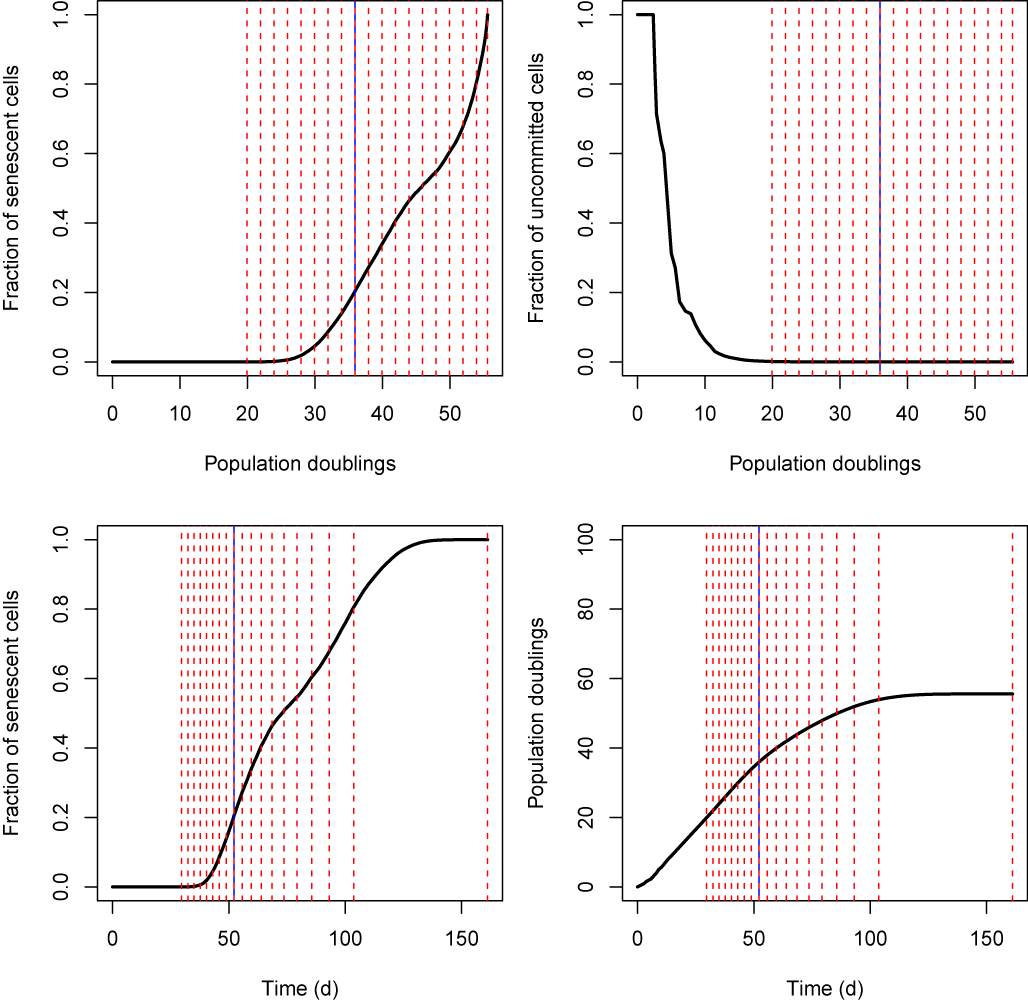Figure 1. Example simulation output for human fibroblast cultures growing to confluence in flasks with a capacity of 1,000,000 cells. Vertical dashed red lines represent time (or population doubling number) at which cells reach confluence, at which stage one eighth of the confluent cells are passaged into a fresh flask. The experiment is initiated with an inoculum of one single uncommitted cell (see commitment theory of Kirkwood & Holliday) which divides to produce two daughter cells. For each daughter of an uncommitted cell, the probability of commitment at each division is 0.275. Newly committed, cells can divide 43 times before becoming senescent. Vertical blue line indicates the time (or population doubling number) at which the final uncommitted cell disappears from the population. Cell division for both uncommitted and committed cells occurs stochastically with a rate of 0.5 divisions per day. The simulation is complete when all cells have undergone replicative senescence and there is no more division.

R package

General overview

This R package consists of a set of functions for:

Reading and formatting data

Simulating transition to replicative senescence